Modèles réduits utilisant les modes non-linéaires

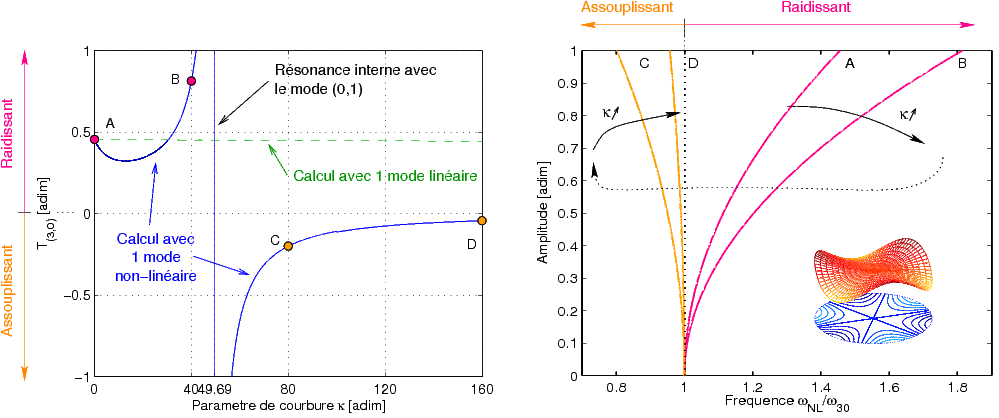
Une des caractéristiques principales de systèmes vibratoires non linéaires géométriques est la dépendance des fréquences caractéristique en l'amplitude des vibrations. En régime forcé, les fréquences de résonances dépendent de l'amplitude, et la même constatation est valable pour les fréquences des oscillations libres. Si, pour un mode donné, ces fréquences augmentent en fonction de l'amplitude, celui-ci est dit raidissant, dans le cas contraire il est assouplissant. Nous avons cherché a prédire ce caractère, en général différent d'un mode à l'autre pour une structure, en utilisant le concept de mode non linéaire. La figure ci-dessous illustre cela : dans le cas d'une coque sphérique, le caractère assouplissant ou raidissant dépend de la courbure de la coque. Notamment, le premier mode à 3 diamètres est raidissant pour les faibles courbures et assouplissant pour les courbures les plus fortes.

Comportement non linéaire du mode (3,0) d'une coque sphérique en fonction de sa courbure. Il est raidissant pour les faibles courbures et devient assouplissant pour les plus fortes courbures.

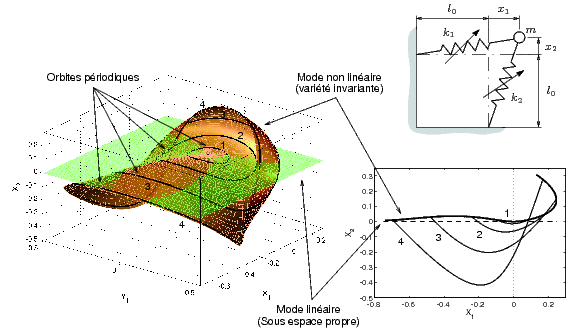
Plus récemment, des calculs numériques de modes non linéaires ont été proposés, par continuation de solutions périodiques. La figure ci-dessous est obtenue avec le logiciel Manlab, dans le cas d'un système masse / ressort non linéaire à deux degrés de libertés. Elle montre la trajectoire du système dans l'espace des phases, ce qui permet de représenter le mode non linéaire comme une variété invariante de cet espace.

Représentation d'un mode non linéaire dans l'espace des phase, sous forme de variété invariante, pour un système à deux degrés de liberté à raideur non linéaire. Calcul obtenu par continuation de solutions périodiques avec le logiciel Manlab.

O. Thomas Col. C. Touzé (ENSTA-UME)