Identification d'excitations déterministes et aléatoires sur une plaque par la méthode des champs virtuels
Au Cnam, Paris, le 2 septembre 2015 à 14h
Alain Berry
Professeur, Groupe d'Acoustique de l'Université de Sherbrooke (GAUS), Québec, Canada
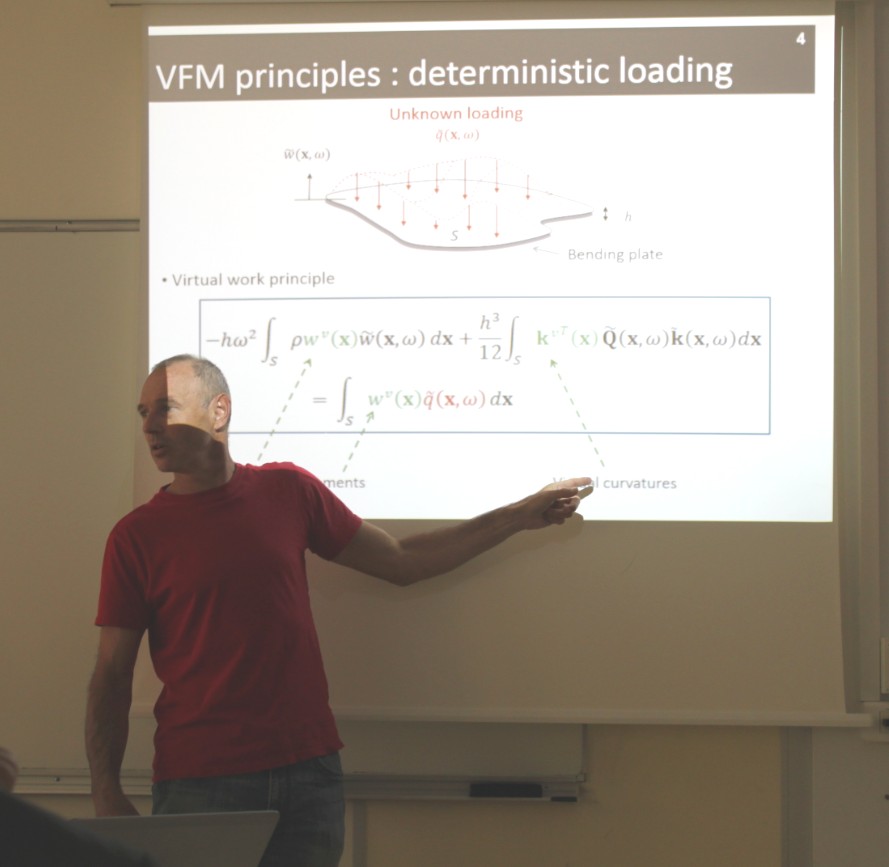
The identification of dynamic forces acting on a structure is an important practical problem in many engineering situations, for instance, to determine dynamic wall pressure fluctuations induced by airflows on vehicles. This work investigates the reconstruction of deterministic and random surface excitations of bending panels from their measured vibration response. The approach employed, called Virtual Fields Method (VFM), starts from an integral form of the plate dynamics (virtual work principle) in which piecewise virtual displacement fields are used to extract the unknown loading over the plate surface. The method therefore requires that the differential operator governing the plate dynamics and its material properties are known a priori. It is fed with the transverse velocity response of the plate measured by Laser Doppler Vibrometry (LDV) over a grid of points. This response is processed to generate both the transverse displacements and bending curvatures necessary to obtain inertial and elastic forces in the integral form of the plate dynamics.
The method was initially implemented to extract spatially deterministic excitations provided by mechanical point forces and acoustical point sources on flexural plates. It has been more recently extended to spatially-correlated excitations such as diffuse acoustic fields and turbulent boundary layers. In these situations, the method allows extracting spatial distributions of loading autospectra and spatial correlations over the plate surface. The presentation will review the principle of the Virtual Fields Method for deterministic and random excitations as well as implementation details. Examples of experimental results will be presented for shaker, acoustic point source and diffuse acoustic field excitations on a test panel.
