Fluid-structure interaction modelization using the enriched space-time finite element
Fluid-structure interaction problems can be stronly non-linear and thus difficult to model specially when thin flexible structures are immersed in a fluid flow as for instance for an artificial cardiac valve. The classical ALE (Arbitrary Lagrangian Eulerian) approach is largely use to treat these problems. However, it has the disadvantage of needed a conforming mesh on the fluid-structure interface: the fluid mesh needs to be updated during the time integration process.
The developed method does not need any remeshing strategy. It is based on a space-time discretization of the coupled problem. The fluid is incompressible, Eulerian and the Navier-Stokes equations are used. One or several thin structures are emmbeded in the fluid using a total Lagrangian formulation. The structures can moved through the fluid fixed space-time mesh, they are catched by the iso-contour of a level set function choosen as the signed distance function to the interface. Embedding a thin structure into the flow field results in non-smooth fields of the physical state variables of the fluid. Based on the concept of the partition of unity and the extended finite element method, the space-time approximations of the fluid pressure and velocity are properly enriched to capture weakly and strongly discontinuous solutions. The enrichment is a Heaviside function based on the sign of the level set function.
 Space-time meshing
|
 Enriched elements
|
Finally, the method leads to a monolithic approach where a non-linear system has to be solved at each time step. The unknowns are fluid velocity and pressure, Lagrange multipliers to ensure velocity continuity at the interface and also structure velocity.
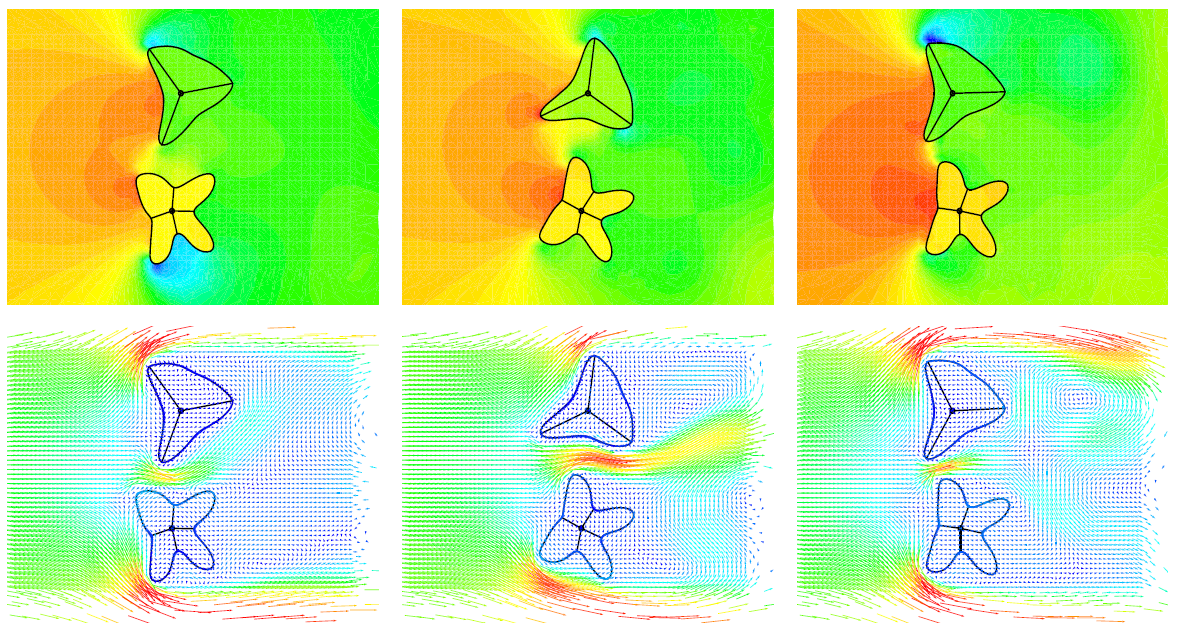
Reference: A. Zilian, A. Legay, The enriched space-time finite element method (EST) for simultaneous solution of fluid-structure interaction, International Journal for Numerical Methods in Engineering, 75 (3), 305-334, 2008. doi
