Modélisation de l'interaction fluide-structure par la méthode des éléments finis espace-temps enrichis
Les problèmes d'interaction fluide-structure sont nombreux et peuvent faire intervenir de fortes non-linéarités notamment quand une structure flexible est immergée dans un écoulement. Les méthodes classiques ALE (Arbitrary Lagrangian Eulerian) sont largement utilisées pour modéliser ces types de problèmes mais elles ont l'inconvénient de nécessiter un remaillage à chaque pas de temps pour assurer la compatibilité des maillages fluide et structure à l'interface.
La méthode développée ici permet de s'affranchir de cette étape de remaillage. Elle est basée sur un maillage éléments finis espace-temps du problème couplé. Le fluide est régi par les équations eulériennes de Navier-Stokes incompressible. Une ou plusieurs structures minces et flexibles sont immergées dans le fluide et sont traitées en Lagrangien total. Les structures évoluent dans le fluide de façon indépendante du maillage espace-temps du fluide qui reste fixe. Chaque structure est suivie par une surface de niveau choisie comme étant la surface signée à l'interface. Basé sur le principe de partition de l'unité
(PuFem, Xfem, ...), les champs d'approximation espace-temps de vitesse et de pression du fluide sont alors enrichis par des fonctions de Heaviside permettant de capter les discontinuités de pression et de vitesse de part et d'autre de la structure.
 Maillage espace-temps
|
 Éléments enrichis
|
La méthode conduit à un système non-linéaire à résoudre à chaque pas de temps comprenant les inconnus de vitesse fluide, pression fluide, multiplicateur de Lagrange assurant la continuité de vitesse à l'interface fluide-structure et enfin vitesse structure.
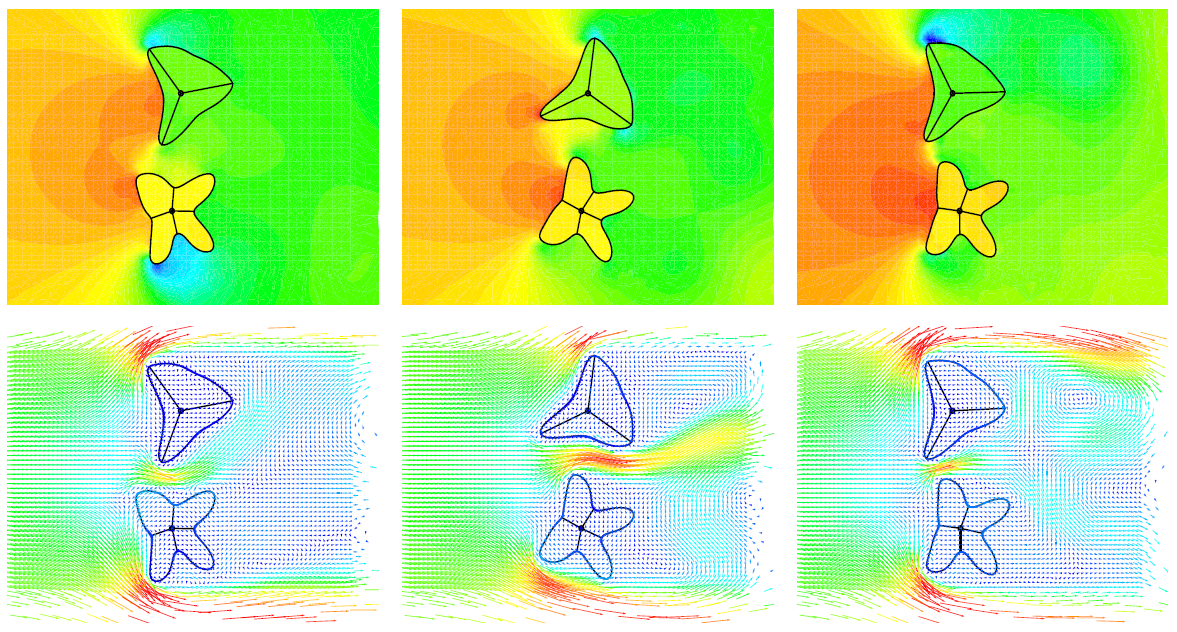
Référence : A. Zilian, A. Legay, The enriched space-time finite element method (EST) for simultaneous solution of fluid-structure interaction, International Journal for Numerical Methods in Engineering, 75 (3), 305-334, 2008. doi
