Filtres Bayésiens parcimonieux - Applications à l'identification d'effort

Les filtres Bayésiens de type Kalman sont utilisés depuis une quinzaine d'années en dynamique des structures pour estimer conjointement ou séquentiellement l'état d'un système ainsi que les efforts qui lui sont appliqués. Lorsque l'on s'intéresse uniquement au problème d'identification d'effort, les filtres faisant références dans la littérature présentent deux défauts majeurs. Le premier concerne le lissage des champs d'efforts reconstruits lorsque la densité de points d'identification devient importante. Le second défaut est lié au phénomène de dérive qui apparaît lorsque seules des mesures d'accélération sont utilisées pour la reconstruction.

Schéma de principe de l'identification d'un champ d'effort appliqué à une structure mécanique

Pour pallier ces problèmes, nous avons développé dans le cadre de la thèse de Julian Ghibaudo, une famille de filtres Bayésien parcimonieux introduisant une contrainte sur la distribution spatiale du champ d'effort à reconstruire. Pour cela, nous nous sommes appuyés sur le paradigme Bayésien pour obtenir une formulation unifiée du problème d'estimation de l'état et de l'excitation d'un système par filtrage Bayésien (de type Kalman).

Cette vision unifiée a permis de montrer que les filtres de la littérature ne diffèrent les uns des autres que par l'hypothèse qu'ils font lors de la prédiction du champ d'excitation à un certain pas de temps et que d'autres filtres peuvent être développé grâce à un choix judicieux de la distribution de probabilité a priori sur le champ d'excitation. À partir de ce constat, nous avons introduit une nouvelle hypothèse supposant que le champ d'excitation prédit (i.e. avant la prise en compte de l'information apportée par une nouvelle mesure) est parcimonieux. Cette hypothèse a permis de développer un filtre dont les performances de reconstruction d'un champ d'effort parcimonieux sont supérieures aux principaux filtres introduits jusque là dans la littérature.

Résultats d'identification d'un coup de marteau sur une plaque en flexion

(a) Montage expérimental	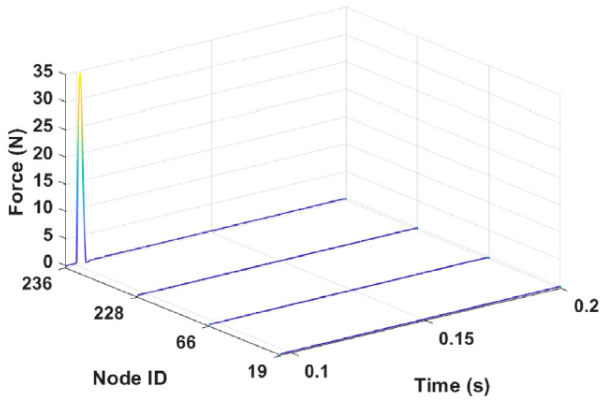(b) Filtre Bayésien proposé
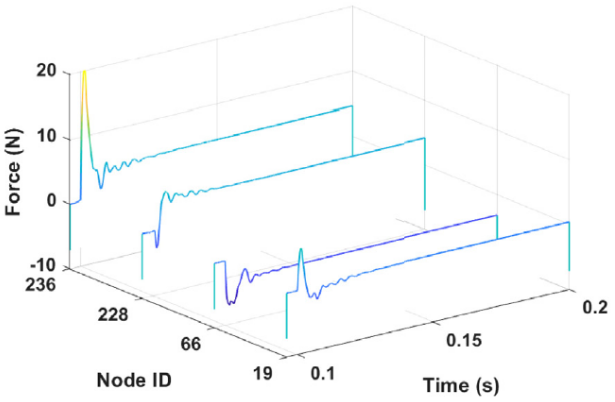(c) Augmented Kalman filter	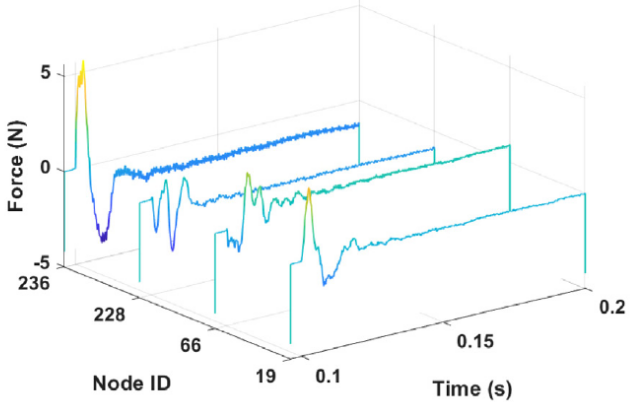(d) Dual Kalman filter